Excel’s Solver is an advanced version of Goal Seek. It’s an excellent tool for making choices between multiple investment options to maximize profit. For example, you can use it to help:
- Choose how much to produce of each product when you have multiple products
- Choose which capital investments to do out of a list of multiple options
Adding Solver
Solver is a Microsoft add-in for Excel. Here are the steps to add it to your Excel:
- Access the Add-Ins:
- Open Excel and click on the “File” tab.
- Select “Options” from the menu.
- Click on “Add-Ins” in the left-hand menu.
- Manage Add-ins:
- In the “Manage” box, choose “Excel Add-ins.”
- Click the “Go” button.
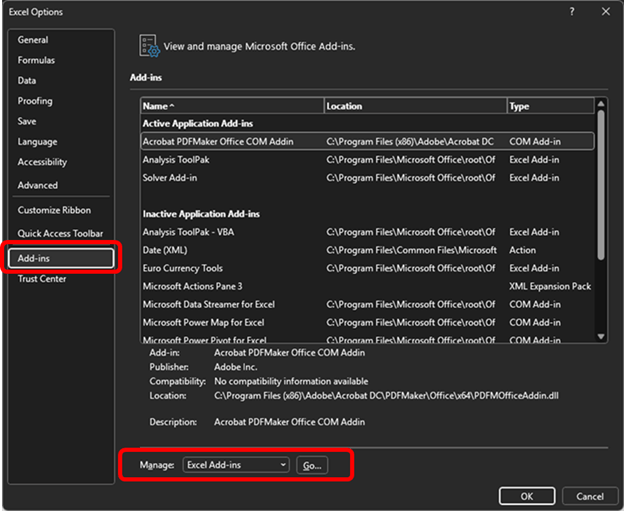
- Select Solver:
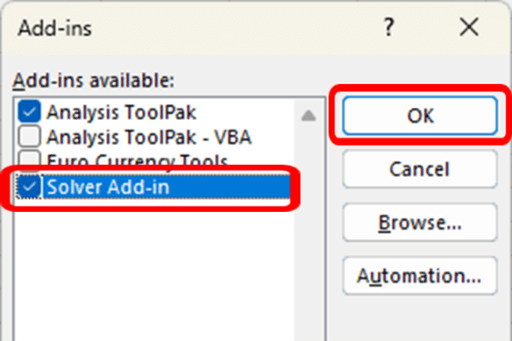
- In the “Add-ins available” box, check the box next to “Solver Add-in.”
- Click “OK” to confirm and activate the Solver Add-in.
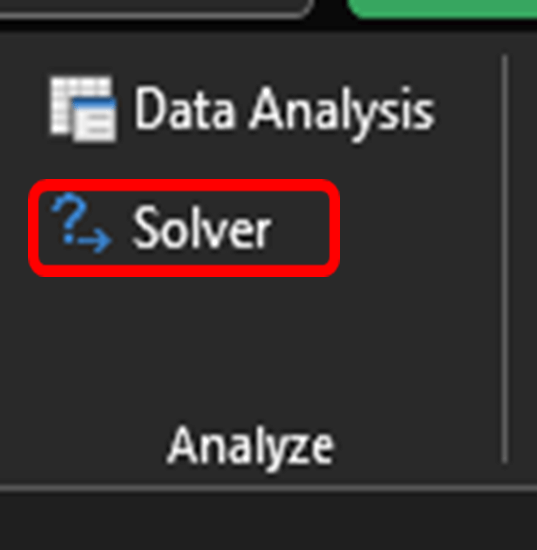
- After activating the Solver add-in, you’ll find the “Solver” command in the “Analysis” group on the “Data” tab.
Using Solver
I’ll walk through using Solver with the example dataset below:
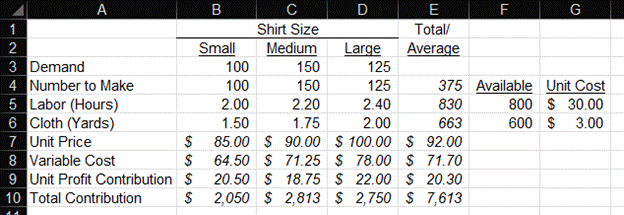
In this example, I’ve left the continuing education business and now serve CPAs by selling them custom dress shirts. You can have your customized shirt in any color you want as long as it’s white. Also, I only sell three sizes of shirts: Small, Medium, and Large.
Here’s a summary of the rows in this analysis:
- Row 3: Demand for my shirts – This is the most I should make.
- Row 4: The number of shirts I should make this month – We will be solving for these cells. For now, I’ve just put the demand amounts from Row 3 into this row.
- Row 5: Labor Hours – This lists the number of hours it takes to make each shirt. I only have five employees, which totals 800 hours of potential labor. Column F shows this constraint. I don’t sew shirts. After years in the corporate world, my skills have atrophied. I can now only manage people and am unable to produce anything of value.
- Row 6: Yard of Cloth – This lists the number of yards of cloth it takes to make each shirt. I only have 600 yards available to me this month. Column F shows this constraint.
- Row 7: Unit Price – This is how much I sell each shirt for.
- Row 8: Variable Cost – This is the variable cost for each shirt.
- Row 9: Unit Contribution – This is Row 7 (Price) minus Row 8 (Cost)
- Row 10: Total Contribution – This is Row 4 (Number to Make) multiplied by Row 9 (Unit Contribution)
You may have noticed that there’s a problem with the numbers I put in Row 4 (Number of Shirts to Make). The total employee hours in Row 5 and the total yards of cloth in Row 6 both exceed my capacity constraints. I can’t find anyone else to work for me, and no one wants to sell me more cloth. Thus, I must produce only the number of shirts that stay within these constraints.
How many of each shirt should I make? It’s time to unleash Solver to answer my dilemma. I select Solver from the Data tab. The Solver Parameters dialog box pops up. Below is how I filled out that dialog box.
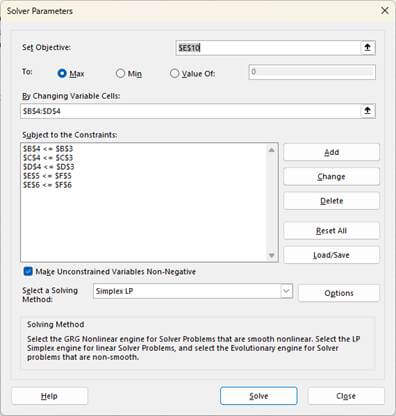
The “Set Objective” box is like the Goal Seek “Set Value” box. The “to” radio buttons allow a minimum or maximum solution to the objective in addition to a set value. Goal Seek doesn’t allow the Max and Min options. In this example, I want to maximize Cell E10, which is the total contribution.
The “By Changing Variable Cells” box is similar to Goal Seek, except that you can specify more than one cell to change. In this example, I’m changing the three cells that specify the number of each shirt size to make.
The “Subject to Constraints” section allows multiple constraints on achieving the objective. I mentioned these earlier. Here are the constraints for this example:
- The first three rows of constraints set the maximum number of each shirt to the demand for that size of shirt.
- The fourth row of constraints sets the maximum total labor to my constraint of 800 hours.
- The fifth row of constraints set the maximum yards of fabric to my constraint of 600 yards.
I set the “Select a Solving Box Method” to Simplex LP since this is a linear problem. You can explore the Options button for this box if you become a pro at using Solver. There are many options to change. I then press my trembling finger on the “Solve” button at the bottom of the dialog box.
In nanoseconds, Excel tells me the phrase that only analysts can truly appreciate: “Solver has found a solution.” This is in the top right corner of the dialog box below. I further bask in the sentences at the bottom of the dialog box that says,” Solver found a solution. All Constraints and optionality conditions are satisfied.” They are satisfied, and I am very satisfied. My shirt production quandary is solved.
If you get a message that says, “Set Values Do Not Converge,” your model has an error or can’t be solved. You likely need to change your constraints or other variables to create a dataset that can be solved.
Before revealing the answers, let’s look at the options in the Results dialog box. I can keep Solver’s solution or revert the number to my original numbers. I can save this as a Scenario.
Solver can also create three reports for me. They provide a lot more detail about the results and the status of the constraint variables. I won’t go into these reports in this short course.
Let’s look at the results from Solver:
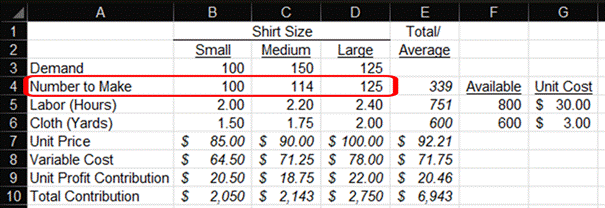
Solver is telling me to make enough shirts to meet the demand for small and large sizes. I then make enough medium shirts until I reach my cloth capacity constraint. I still have some slack in labor hours.
From here, I could do more modeling to optimize production. I could find out how many yards of cloth to buy next month so I can maximize my labor hours and contribution. I may re-run this with adjusted price and demand numbers.
Some people may have looked at my dataset and thought that the intuitive course of action was to maximize large shirts because they have the highest contribution, and then make small shirts, and then the low-margin medium shirts. This intuition doesn’t factor in the consumption of my constraints. I lowered the cloth constraint to 300 yards to see what Solver recommends:
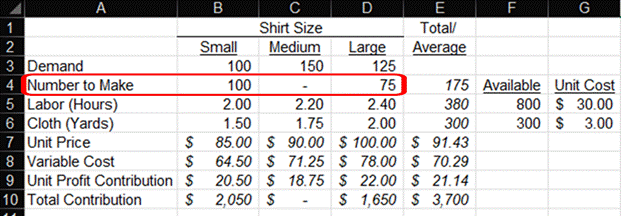
Solver shows us that we want to fill the demand for small shirts before making the large shirts. The contribution of a small shirt is lower than that of a large shirt, but they use the constraints more efficiently for the contribution they provide.
Of course, we probably wouldn’t want to make just lots of small shirts and no medium shirts. This wouldn’t be good for customer satisfaction in the long run. I could amend the Solver to add constraints for the minimum number of each shirt to make.
For more info, check out these topics pages:
